Delay Calibration

Delay Center Calibration

1. Background

Figure 1: EOVSA data in the 12.15-12.55 GHz band on CIEL-2, taken with nearly optimal delay (in this case -7 steps in Y relative to X channel) on Antenna 4 in R (blue) and L (green) polarizations. The channels and their polarizations agree well with the nominal band centers, shown with the blue and green vertical lines. Each channel is relatively flat, and separated by narrow notches, but the R and L bands overlap in an interleaving fashion. The band amplitudes vary because the transmissions are in “spot beams” pointed at different places in North America, not all pointing directly at central California.

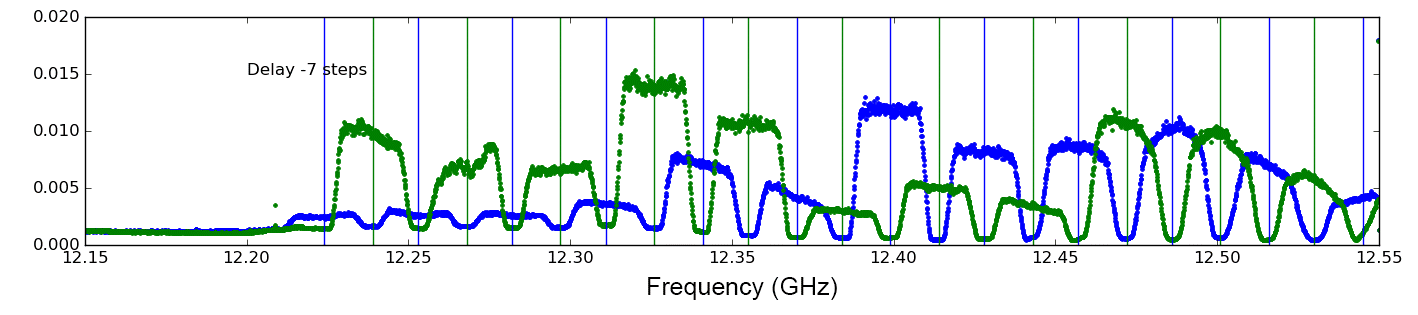
The signals from each antenna have to reach the correlator with the appropriate delays to compensate for cable length differences. For most interferometers, only relative delays between antennas matters, but because the EOVSA converts X and Y polarization into R and L, it appears that the relative delay requirement between X and Y for a given antenna is even more stringent (see section 2). The problem is especially tricky for EOVSA, because the ROACH boards use the KatADC digitizers, which have a clock speed that is a factor of 4 higher than the FPGA clock, so that four-way multiplexing is done. The initialization of this multiplexing is random on startup of the ROACH boards, so there can be differences of up to 4 coarse delay steps, which has to be calibrated every time the ROACHes are restarted. Thus, we need a delay center calibration procedure that can be done quickly and reliably. This document describes the use of geostationary satellites for delay center calibration, as well as some lessons learned by using this method. This concerns both interferometric phase on each baseline and polarization purity on each antenna, but both can be accomplished at the same time by choosing a satellite with both R and L polarized channels. The precise analysis needed depends strongly on the choice of geostationary satellite. The experiments done so far have used the CIEL-2 satellite, which has alternating R- and L-polarized channels that overlap. The transmission bands of CIEL-2 are well demonstrated by the actual EOVSA total power data shown in Figure 1. The CIEL-2 satellite is located at $149^{o}$ W longitude, and so is fairly isolated from other satellites, which become close together at more eastern longitudes. It is good to avoid having more than one satellite in the 2.1-m antenna beam at a time. The EOVSA beam is relatively small at this $K_{u}$ band frequency, which also helps.

Figure 2: R-channel amplitudes taken on CIEL-2 while stepping Y-channel delays relative to X by one step/s. The alternation between R and L on every step is seen at high channel numbers, while it takes two steps to swtich at channel 2048, and four steps at channel 1024. The optimum step is around 0.5.

To observe a geostationary satellite with the EOVSA system is quite easy. The system automatically downloads the latest coordinate (two-line element, or TLE) files from http://www.celestrak.com/, finds the satellite name in the file, and converts the TLE coordinates to the required RA and Dec table needed to track the satellite. The satellite name for CIEL-2 is just CIEL-2, but because the names have to match exactly, it is sometimes necessary to manually download the file http://www.celestrak.com/NORAD/elements/geo.txt and find the exact spelling of the satellite name. If there are spaces in the name (e.g. “GALAXY 3C (G-3C)”), replace them with underscores (“GALAXY_3C_(G-3C)”). Because these are geostationary satellites, when the track tables are loaded into the antennas the RA should advance 1 s for each second, in order to keep the actual position fixed. However, the satellites do execute small ellipses on the sky, so RA and Dec do change very slightly.

2. Delay Centers and R/L Polarization

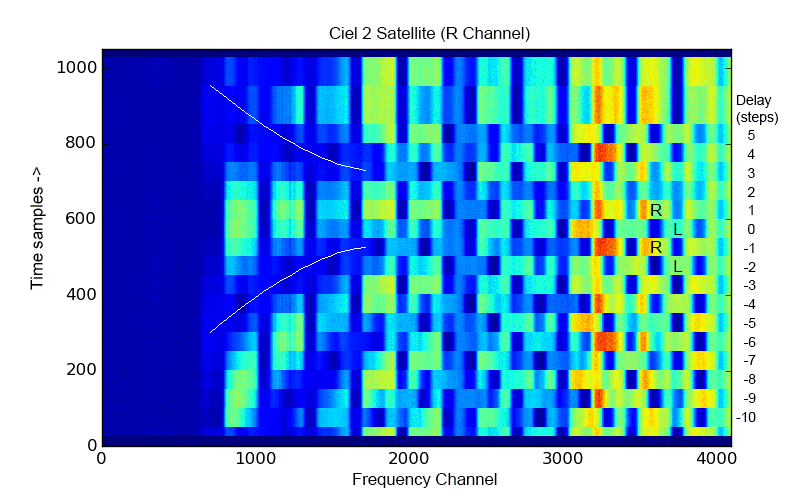
Because the R and L polarization is obtained from X and Y in the digital correlator, the delays between X and Y channels must be kept very close to zero. In fact, for Nyquist sampling of the IF that we use, a single coarse delay step at the high end corresponds to a complete swap of polarization R -> L and L -> R. This is nicely demonstrated by Figure 2, which shows data taken on the Ciel-2 geostationary satellite in R polarization. As shown in Figure 1, the broadcast frequencies on this satellite alternate between R and L polarization. As the delay is swept from -10 steps to +5 steps, the polarization pattern, which nominally should look like the one at delay step +1, instead alternates between R and L polarization on each step at frequency channel 4096, but takes two steps at channel 2048, and four steps at channel 1024, etc. The alternation at lower channels produces a symmetric pattern suggested by the two white curves overlaid on the plot, and helps to show that the best step will be somewhere between steps 1 and 0, but closer to step 1. Unfortunately, to get the correct delay within less than a coarse delay step requires either the insertion of a small length of cable equivalent to the desired partial-step delay, or else an adjustment of the complex number used in the correlator to convert X and Y to R and L.

Figure 3: Plots of the data in Figure 2 at close to the optimal delay and at the adjacent delay offsets above and below it. Note that the color of the channels near 12.5 GHz (180-degrees per step) alternate while those near 12.2 GHz do not. At 12.35 GHz, the top plot is X,Y, middle plot is R,L, and bottom plot is Y,X, etc., as the phase drift caused by the delay is 90-degrees per step.

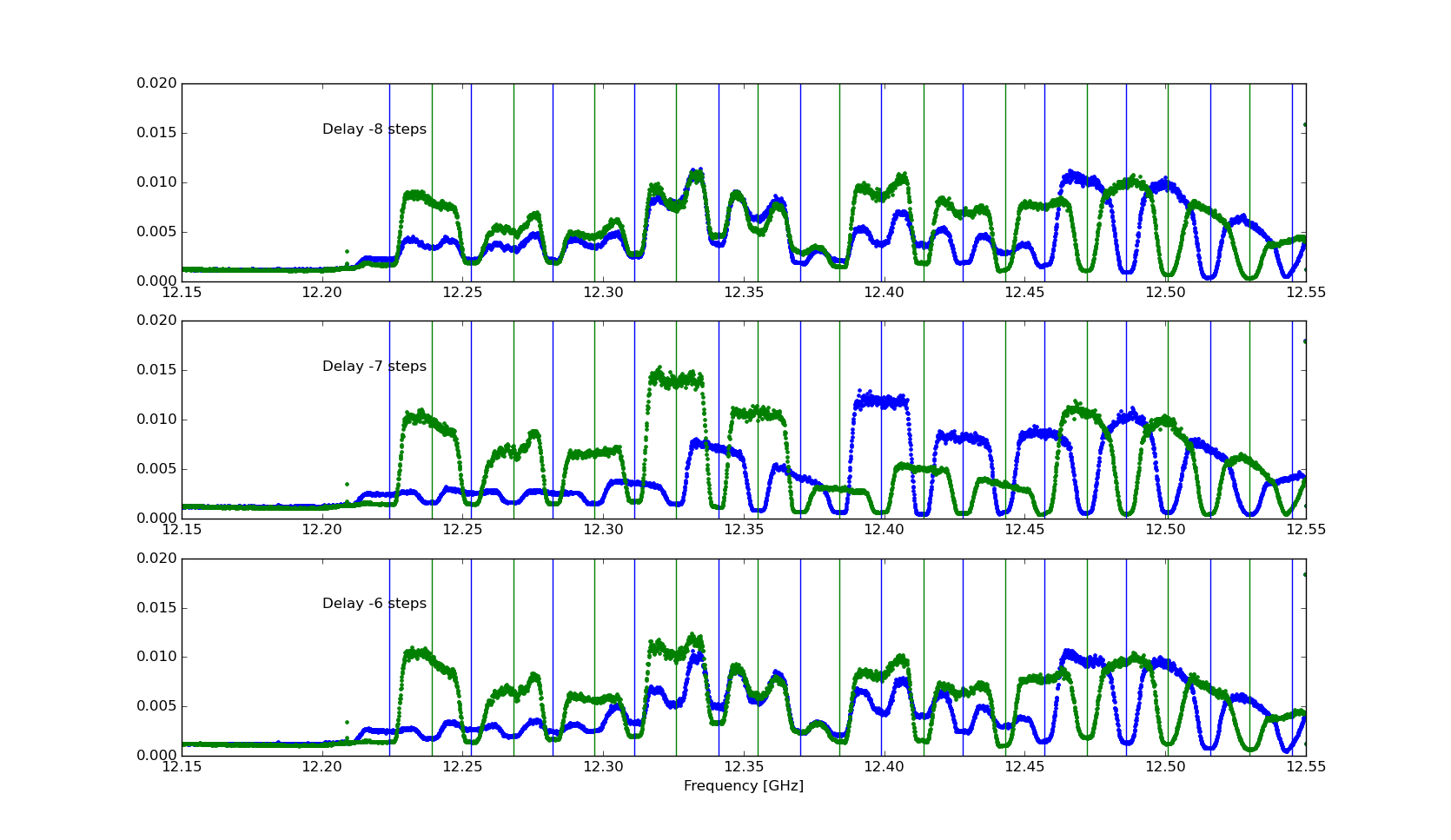
In the case of Figure 2, the optimum delay of Y with respect to X is about +0.5 steps, which can be accomplished by adding an approximately 6-inch cable in the Y-channel, calculated from (0.5 step)*(1.25 ns/step)*(0.85 ft/ns), where the latter factor takes into account the slower propagation of light in cable. Note that only fractional steps need to be adjusted by adding short cables, since whole steps can be adjusted simply by adjusting the coarse delay offsets in the file delay_centers.txt. For example, the data shown in Figure 3 are the same as in Figure 2, but taken at a time when the optimal delay was 7 steps off. Instead of adding short cables, it is likely that merely adjusting the complex factor used to convert X, Y to R, L in the correlator can be adjusted for the appropriate delay (i.e. instead of a constant, an appropriate slope in phase correction can be introduced), but I think it is best for now to try to get an optimized analog system so that any such phase corrections are either not needed or kept small. Whenever the ROACH boards are power-cycled or restarted, we can expect the phase of the 4-way multiplexing of the digitized signal to change randomly between 0, 1, 2, and 3 in units of coarse steps. Because the two polarizations of each antenna go through the same digitizer, it may be that the two channels of a given digitizer change their multiplexing phase together, in which case the relative X and Y delay will not change. This remains to be confirmed. If so, an analysis like the above is only needed on an occasional basis in case some analog component or cable changes. If the X and Y multiplexing phases do change independently, then the above analysis will have to be done on each restart.

3. Delay Centers and Cross-Correlation

The above considerations affect the relative X vs. Y delays on a given antenna. In addition, the overall delays of X on each antenna relative to X on the others, and likewise for Y, have to be maintained at the optimum value by examining the slope in phase across the band while on a satellite. Note that the cross-correlation measurements are completely independent in X and Y, so optimal delays from cross-correlation do not guarantee optimal delays for the purpose of polarization as described above. In fact, it is probably best to do cross-correlation optimization using the correlator in X and Y mode rather than R and L, to avoid conflating the two.