Delay Calibration: Difference between revisions
| (4 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
== Practical Delay Setting == | == Practical Delay Setting == | ||
Whenever the ROACH boards (correlator) are rebooted, new delays have to be determined. Here is a practical guide to doing that. The broad steps are: | Whenever the ROACH boards (correlator) are rebooted, new delays have to be determined. Here is a practical guide to doing that. The broad steps are: | ||
* Point the antennas at the geosynchronous satellite | * Point the antennas at the geosynchronous satellite ECHO (with suitable attenuation to keep the receivers from overloading) | ||
* Capture 1 second of data for analysis | * Capture 1 second of data for analysis | ||
* Analyze the data to find rough delay values | * Analyze the data to find rough delay values | ||
| Line 12: | Line 12: | ||
Below are details of each step. | Below are details of each step. | ||
=== Point the antennas at geosynchronous satellite | === Point the antennas at geosynchronous satellite ECHO === | ||
This is easily accomplished using the schedule file ''' | This is easily accomplished using the schedule file '''geosat_echo_kband.scd'''. Load this file into the schedule (it tracks a single source for 24 h) and hit the Today button to update the date, then hit GO. This will track the satellite with all antennas, enter the appropriate attenuations, and start the kband.fsq sequence. NB: The data system will not start recording the data--instead we capture the data in the next step. | ||
=== Capture 1 second of data === | === Capture 1 second of data === | ||
| Line 20: | Line 20: | ||
=== Analyze the data to find rough delay values === | === Analyze the data to find rough delay values === | ||
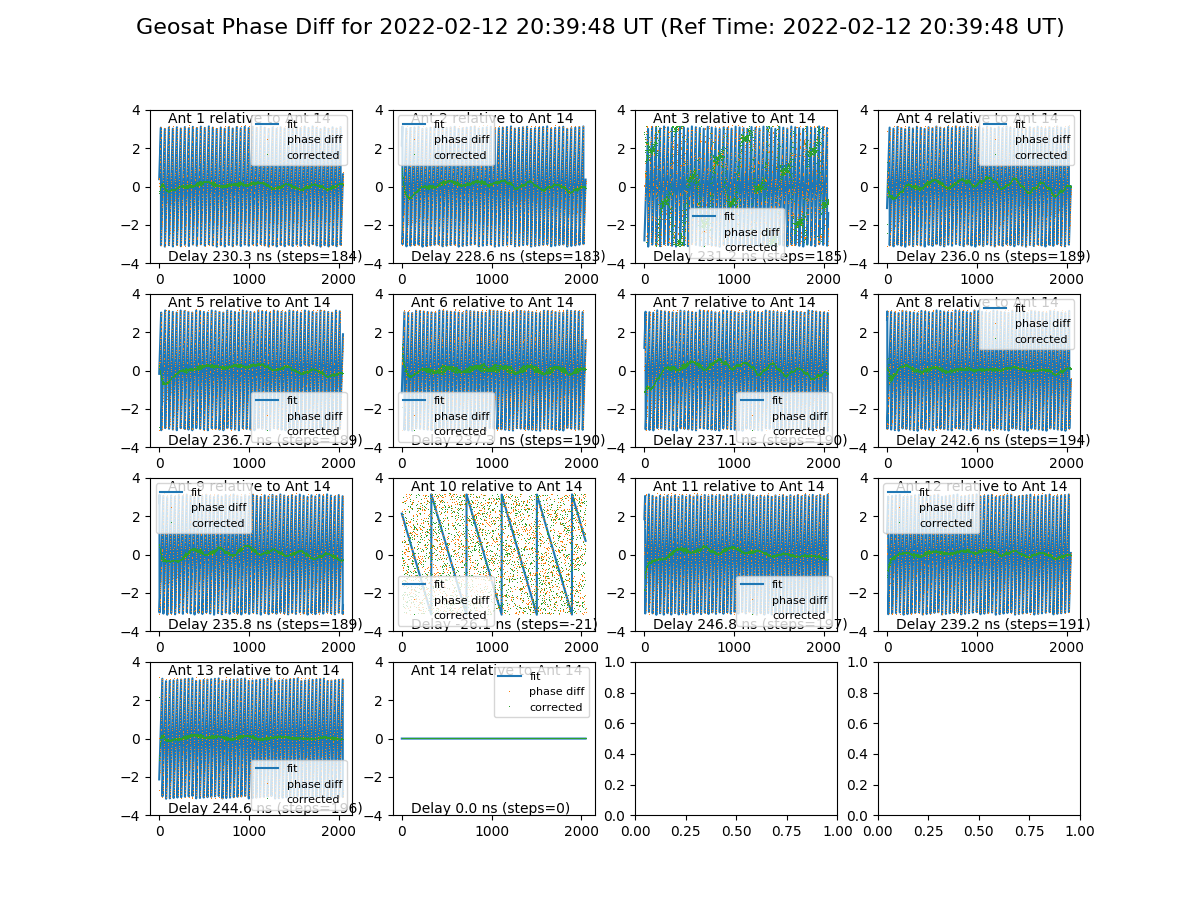
[[File:sat_delays.png|thumb|400px| '''Figure 1:''' Plot of the phase relative to Ant | [[File:sat_delays.png|thumb|400px| '''Figure 1:''' Plot of the phase relative to Ant 14 for data taken on the satellite CIEL-2 on 2022-02-12. Each panel shows the phase in radians vs. fine frequency channel (red), a linear phase slope fit (blue), and the difference between data and fit (green). In this case there is a huge delay for antenna 14 and antenna 10 was not tracking.]] | ||
On the Pipeline computer get into ipython and issue the following commands: | On the Pipeline computer get into ipython and issue the following commands: | ||
import pcapture2 as p | import pcapture2 as p | ||
out = p.rd_jspec('/dppdata1/PRT/PRT<yyyymmddhhmmss>geo.dat') | out = p.rd_jspec('/dppdata1/PRT/PRT<yyyymmddhhmmss>geo.dat') | ||
p.prt_dla(out, ref=None, refant= | p.prt_dla(out, ref=None, refant=14, doplot=True) | ||
This will print a table of delays relative to antenna | This will print a table of delays relative to antenna 14 to the screen as below (asterisks mark values with high standard deviation) and also plot the result as in Figure 1: | ||
Ant: 1 Steps: | Ant: 1 Steps: 184.2 stdev [deg]: 6.7 Delay [ns]: 230.310 | ||
*Ant: 2 Steps: 183.0 stdev [deg]: 12.0 Delay [ns]: 228.688 | |||
*Ant: 3 Steps: 185.0 stdev [deg]: 101.0 Delay [ns]: 231.247 | |||
*Ant: 4 Steps: | *Ant: 4 Steps: 188.8 stdev [deg]: 15.3 Delay [ns]: 236.018 | ||
*Ant: 5 Steps: | *Ant: 5 Steps: 189.4 stdev [deg]: 13.7 Delay [ns]: 236.759 | ||
Ant: 6 Steps: | Ant: 6 Steps: 189.8 stdev [deg]: 9.2 Delay [ns]: 237.302 | ||
*Ant: 7 Steps: | *Ant: 7 Steps: 189.7 stdev [deg]: 19.3 Delay [ns]: 237.145 | ||
Ant: 8 Steps: 194.1 stdev [deg]: 7.7 Delay [ns]: 242.625 | |||
*Ant: 9 Steps: | *Ant: 9 Steps: 188.7 stdev [deg]: 11.6 Delay [ns]: 235.863 | ||
*Ant: 10 Steps: | *Ant: 10 Steps: -20.9 stdev [deg]: 104.9 Delay [ns]: -26.142 | ||
*Ant: 11 Steps: | *Ant: 11 Steps: 197.5 stdev [deg]: 13.4 Delay [ns]: 246.862 | ||
Ant: 12 Steps: | Ant: 12 Steps: 191.4 stdev [deg]: 8.6 Delay [ns]: 239.295 | ||
Ant: 13 Steps: 195.7 stdev [deg]: 5.4 Delay [ns]: 244.629 | |||
Ant: 14 Steps: | Ant: 14 Steps: 0.0 stdev [deg]: 0.0 Delay [ns]: 0.000 | ||
Note that the delays get quite far off for the higher-numbered antennas--not sure why | The delays that would be tried in delay_widget.py are those in the last column. Note that in this case the Ant 14 delay was way off, so it shows up as huge delays in all antennas because these are delays with respect to the erroneous Ant 14. Note also that the delays get quite far off for the higher-numbered antennas--not sure why. | ||
== Background == | == Background == | ||
Latest revision as of 16:57, 16 October 2024
Delay Center Calibration
Practical Delay Setting
Whenever the ROACH boards (correlator) are rebooted, new delays have to be determined. Here is a practical guide to doing that. The broad steps are:
- Point the antennas at the geosynchronous satellite ECHO (with suitable attenuation to keep the receivers from overloading)
- Capture 1 second of data for analysis
- Analyze the data to find rough delay values
- If there are large delays, run delay_widget.py to adjust the delays in a "blind" mode
- Take at least 20 min of data on a calibrator
- Run delay_widget.py to fine tune the delays
- As soon as possible, run the X-Y delay calibration procedure on source 2253+161
Below are details of each step.
Point the antennas at geosynchronous satellite ECHO
This is easily accomplished using the schedule file geosat_echo_kband.scd. Load this file into the schedule (it tracks a single source for 24 h) and hit the Today button to update the date, then hit GO. This will track the satellite with all antennas, enter the appropriate attenuations, and start the kband.fsq sequence. NB: The data system will not start recording the data--instead we capture the data in the next step.
Capture 1 second of data
After all antennas are tracking (Ant 12 for some reason does not like to track exactly on a geosat, so you may have to ignore small errors there), then send the command $capture-1s geo from the Raw Command of the schedule. After about 10-15 s, the capture file should appear in the DPP on /disk1/PRT/PRT<yyyymmddhhmmss>geo.dat.
Analyze the data to find rough delay values
On the Pipeline computer get into ipython and issue the following commands:
import pcapture2 as p
out = p.rd_jspec('/dppdata1/PRT/PRT<yyyymmddhhmmss>geo.dat')
p.prt_dla(out, ref=None, refant=14, doplot=True)
This will print a table of delays relative to antenna 14 to the screen as below (asterisks mark values with high standard deviation) and also plot the result as in Figure 1:
Ant: 1 Steps: 184.2 stdev [deg]: 6.7 Delay [ns]: 230.310 *Ant: 2 Steps: 183.0 stdev [deg]: 12.0 Delay [ns]: 228.688 *Ant: 3 Steps: 185.0 stdev [deg]: 101.0 Delay [ns]: 231.247 *Ant: 4 Steps: 188.8 stdev [deg]: 15.3 Delay [ns]: 236.018 *Ant: 5 Steps: 189.4 stdev [deg]: 13.7 Delay [ns]: 236.759 Ant: 6 Steps: 189.8 stdev [deg]: 9.2 Delay [ns]: 237.302 *Ant: 7 Steps: 189.7 stdev [deg]: 19.3 Delay [ns]: 237.145 Ant: 8 Steps: 194.1 stdev [deg]: 7.7 Delay [ns]: 242.625 *Ant: 9 Steps: 188.7 stdev [deg]: 11.6 Delay [ns]: 235.863 *Ant: 10 Steps: -20.9 stdev [deg]: 104.9 Delay [ns]: -26.142 *Ant: 11 Steps: 197.5 stdev [deg]: 13.4 Delay [ns]: 246.862 Ant: 12 Steps: 191.4 stdev [deg]: 8.6 Delay [ns]: 239.295 Ant: 13 Steps: 195.7 stdev [deg]: 5.4 Delay [ns]: 244.629 Ant: 14 Steps: 0.0 stdev [deg]: 0.0 Delay [ns]: 0.000
The delays that would be tried in delay_widget.py are those in the last column. Note that in this case the Ant 14 delay was way off, so it shows up as huge delays in all antennas because these are delays with respect to the erroneous Ant 14. Note also that the delays get quite far off for the higher-numbered antennas--not sure why.
Background
The signals from each antenna have to reach the correlator with the appropriate delays to compensate for cable length differences. For most interferometers, only relative delays between antennas matters, but because the EOVSA converts X and Y polarization into R and L, it appears that the relative delay requirement between X and Y for a given antenna is even more stringent (see section 2). The problem is especially tricky for EOVSA, because the ROACH boards use the KatADC digitizers, which have a clock speed that is a factor of 4 higher than the FPGA clock, so that four-way multiplexing is done. The initialization of this multiplexing is random on startup of the ROACH boards, so there can be differences of up to 4 coarse delay steps, which has to be calibrated every time the ROACHes are restarted. Thus, we need a delay center calibration procedure that can be done quickly and reliably.
This document describes the use of geostationary satellites for delay center calibration, as well as some lessons learned by using this method. This concerns both interferometric phase on each baseline and polarization purity on each antenna, but both can be accomplished at the same time by choosing a satellite with both R and L polarized channels.
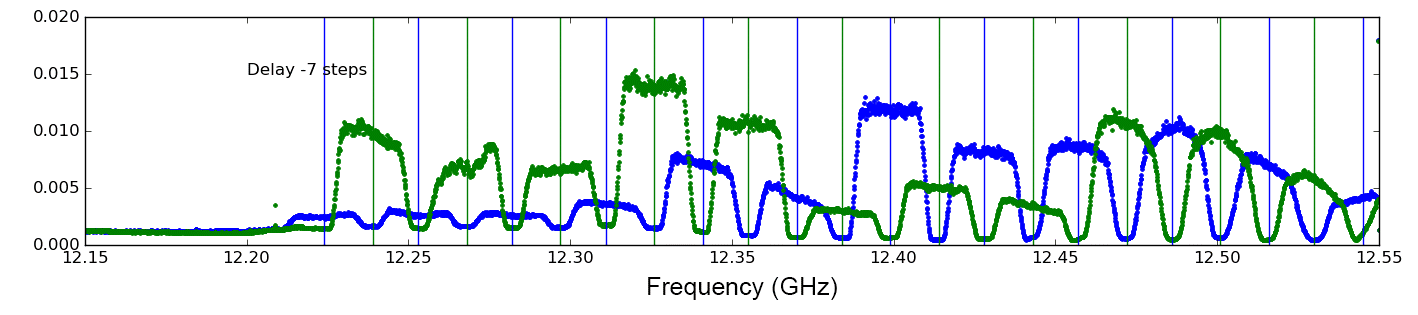
The precise analysis needed depends strongly on the choice of geostationary satellite. The experiments done so far have used the CIEL-2 satellite, which has alternating R- and L-polarized channels that overlap. The transmission bands of CIEL-2 are well demonstrated by the actual EOVSA total power data shown in Figure 1.
The CIEL-2 satellite is located at W longitude, and so is fairly isolated from other satellites, which become close together at more eastern longitudes. It is good to avoid having more than one satellite in the 2.1-m antenna beam at a time. The EOVSA beam is relatively small at this band frequency, which also helps.
To observe a geostationary satellite with the EOVSA system is quite easy. The system automatically downloads the latest coordinate (two-line element, or TLE) files from http://www.celestrak.com/, finds the satellite name in the file, and converts the TLE coordinates to the required RA and Dec table needed to track the satellite. The satellite name for CIEL-2 is just CIEL-2, but because the names have to match exactly, it is sometimes necessary to manually download the file http://www.celestrak.com/NORAD/elements/geo.txt and find the exact spelling of the satellite name. If there are spaces in the name (e.g. “GALAXY 3C (G-3C)”), replace them with underscores (“GALAXY_3C_(G-3C)”). Because these are geostationary satellites, when the track tables are loaded into the antennas the RA should advance 1 s for each second, in order to keep the actual position fixed. However, the satellites do execute small ellipses on the sky, so RA and Dec do change very slightly.
Delay Centers and R/L Polarization
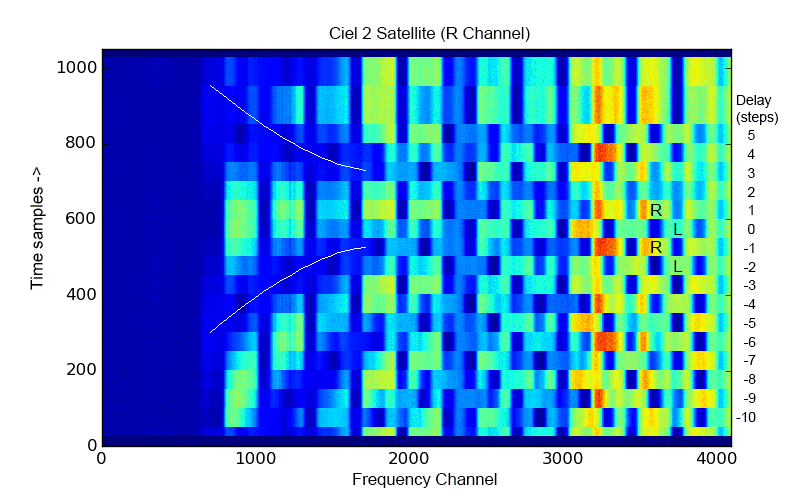
Because the R and L polarization is obtained from X and Y in the digital correlator, the delays between X and Y channels must be kept very close to zero. In fact, for Nyquist sampling of the IF that we use, a single coarse delay step at the high end corresponds to a complete swap of polarization R -> L and L -> R. This is nicely demonstrated by Figure 2, which shows data taken on the Ciel-2 geostationary satellite in R polarization. As shown in Figure 1, the broadcast frequencies on this satellite alternate between R and L polarization. As the delay is swept from -10 steps to +5 steps, the polarization pattern, which nominally should look like the one at delay step +1, instead alternates between R and L polarization on each step at frequency channel 4096, but takes two steps at channel 2048, and four steps at channel 1024, etc. The alternation at lower channels produces a symmetric pattern suggested by the two white curves overlaid on the plot, and helps to show that the best step will be somewhere between steps 1 and 0, but closer to step 1. Unfortunately, to get the correct delay within less than a coarse delay step requires either the insertion of a small length of cable equivalent to the desired partial-step delay, or else an adjustment of the complex number used in the correlator to convert X and Y to R and L.
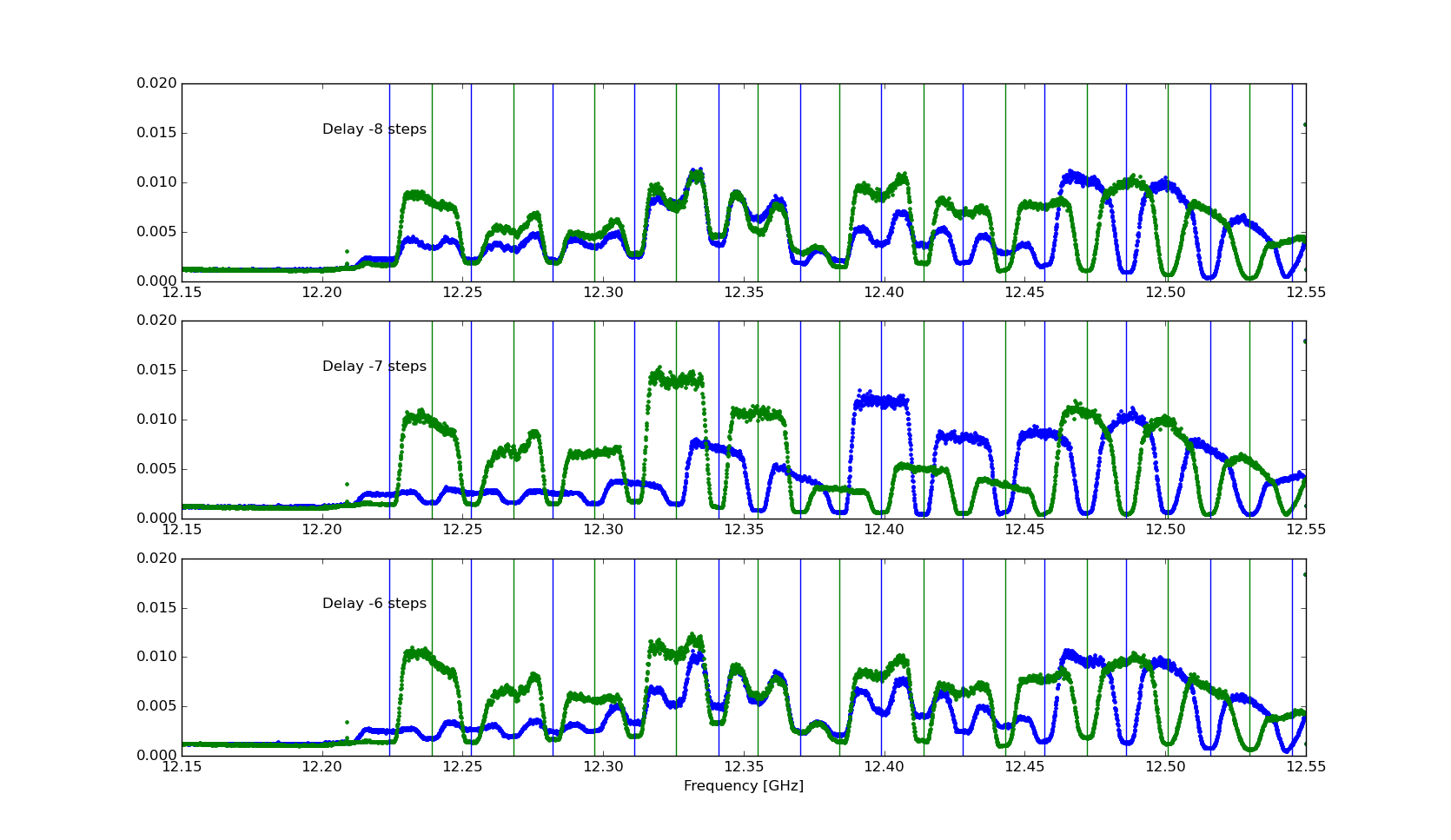
In the case of Figure 2, the optimum delay of Y with respect to X is about +0.5 steps, which can be accomplished by adding an approximately 6-inch cable in the Y-channel, calculated from (0.5 step)*(1.25 ns/step)*(0.85 ft/ns), where the latter factor takes into account the slower propagation of light in cable. Note that only fractional steps need to be adjusted by adding short cables, since whole steps can be adjusted simply by adjusting the coarse delay offsets in the file delay_centers.txt. For example, the data shown in Figure 3 are the same as in Figure 2, but taken at a time when the optimal delay was 7 steps off.
Instead of adding short cables, it is likely that merely adjusting the complex factor used to convert X, Y to R, L in the correlator can be adjusted for the appropriate delay (i.e. instead of a constant, an appropriate slope in phase correction can be introduced), but I think it is best for now to try to get an optimized analog system so that any such phase corrections are either not needed or kept small.
Whenever the ROACH boards are power-cycled or restarted, we can expect the phase of the 4-way multiplexing of the digitized signal to change randomly between 0, 1, 2, and 3 in units of coarse steps. Because the two polarizations of each antenna go through the same digitizer, it may be that the two channels of a given digitizer change their multiplexing phase together, in which case the relative X and Y delay will not change. This remains to be confirmed. If so, an analysis like the above is only needed on an occasional basis in case some analog component or cable changes. If the X and Y multiplexing phases do change independently, then the above analysis will have to be done on each restart.
Delay Centers and Cross-Correlation
The above considerations affect the relative X vs. Y delays on a given antenna. In addition, the overall delays of X on each antenna relative to X on the others, and likewise for Y, have to be maintained at the optimum value by examining the slope in phase across the band while on a satellite. Note that the cross-correlation measurements are completely independent in X and Y, so optimal delays from cross-correlation do not guarantee optimal delays for the purpose of polarization as described above. In fact, it is probably best to do cross-correlation optimization using the correlator in X and Y mode rather than R and L, to avoid conflating the two.
Fine Delay Calibration
1. Background
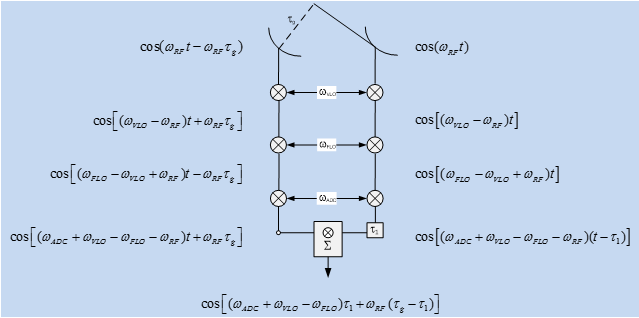
This document describes the principles to be considered for fine delay correction of EOVSA correlated data. It will be helpful to refer to the memo Documentation of Downconversion and Tuning, which describes the three consecutive frequency-conversion operations required to tune and isolate a clean 500 MHz IF band from the 1-18 GHz RF band. We will refer to several frequencies in this document, defined below:
angular frequency of the RF, which nominally ranges over
angular frequency of the variable (tuning) LO, which ranges over
angular frequency of the fixed LO, which is
angular frequency of the ADC clock, which is now -> will be
Note that for EOVSA’s nominal operation, has only discrete values corresponding to frequencies GHz, while varies continuously. The tuning of to these discrete values provides the 500-MHz-wide bands labeled as integers (1-34) in the scan header as FSeqList. The relationship between the band numbers in FSeqList and in GHz is
This discussion will follow the discussion in Appendix A of Liu et al. (2007), see Figure 1 below.
As shown in Figure 1, a plane wave arrives later for the antenna on the left, so its fluctuating waveform is shifted by a phase , where is the continuously varying geometric delay required to track the source. The first downconversion by the variable LO inverts the frequencies on both antennas and shifts them by the oscillator frequency . The second downconversion by the fixed LO inverts and shifts the frequencies by in a similar manner. This produces an IF frequency in the range 600-1200 MHz. The final downconversion is done by the ADC, which does a final inversion of the frequencies and shifts them by . After digitization, an integer “course delay” rounded to the nearest digitizer clock step, is inserted into the right-hand antenna. After correlation (multiplication and averaging), the fast fluctuation involving t is eliminated, but the signal is left with a fluctuating phase (2) where is the non-integer “fine delay,” which must be applied on a channel-by-channel basis across the 600 MHz IF band, while the first term is constant over the band (for a given tuning frequency). The phase in equation (2) is to be subtracted from the phase of the baseline.
2, Cross-Checks
To verify that the above is correct, first note that the frequency (3) is the IF frequency corresponding to RF frequency . As shown in the memo Documentation of Downconversion and Tuning, (see Figure 2, reproduced from that document) for an ADC clock frequency of 1200 MHz, we expect (blue numbers in Figure 2) an RF frequency of, say, 2.5 GHz, to be at IF frequency 50 MHz when tuned to the 2-2.5 GHz band (FSeqList = 3), while the other end of the band, 2.0 GHz, should be at 550 MHz (i.e. the IF band is inverted relative to the RF).
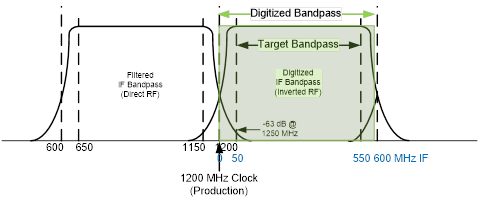
Using equation (1), the variable LO would be tuned to 22.5 GHz for this band, so:
, .
The equation (3) works for any band, when and are changed appropriately. Likewise, if the ADC clock frequency is 800 MHz, as it is at present, then the lower part of the band (0-200 MHz) is overlapped, and the upper part of the band (200-400 MHz) is direct relative to the RF (see Figure 3, reproduced from the earlier memo).
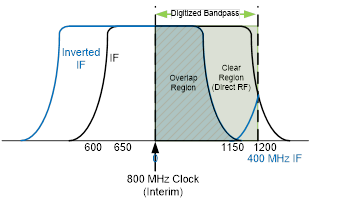
In this case, for the same 2.0-2.5 GHz band 3 as the earlier example, we expect 2.0 GHz RF to be at 150 MHz IF, 2.15 GHz to be at 0 MHz IF, 2.3 GHz to be again at 150 MHz, and 2.5 GHz RF to be at 350 MHz. For these four cases, equation (2) gives:
, , , .
Note that any RF frequency above 2.15 GHz results in a negative IF frequency, which, when aliased about zero, becomes the absolute value of the IF frequency. We conclude that equation (3) is accurate for any ADC clock and RF frequency. Looking now at equation (2), the first term is the phase variation associated with natural fringes, while the second term is the channel-dependent phase associated with the “fine delay” (the difference between integer-stepped “coarse delay” and the true geometric delay). Let us look at these terms and verify that they have the expected behavior. Let’s rewrite this as:
.
The first term, , is constant for a given band, and by definition constant over a 1-s period since delay steps can only happen on 1-s boundaries. In fact, this term can remain constant for several minutes for short baselines that are not changing projected length very fast. The term can grow very large, and has stepwise discontinuities since varies in “coarse delay” steps. Because ranges from 21.5-38 GHz, for the case of an 800 MHz ADC clock the frequency term ranges from 7.226 radians/ns to 110.898 radians/ns (414-6354 degrees/ns). Since the steps in occur in 1.25 ns steps for an 800 MHz ADC clock, this is 517.5-7942.5 degrees/step. Although this seems large, it agrees with my analysis detailed in section 2.1 Delay Tracking, in the memo EOVSA_Calibration. There I found a maximum fringe rate of 6.6 Hz. Taking 6354 degrees/ns, and maximum delay rate of 0.364 ns/s from that memo, I have (6354 degrees/ns) (0.364 ns/s) / (360 degrees) = 6.44 Hz. The slight discrepancy is due to the above numbers referring to a frequency of 17.650 GHz (see next paragraph), whereas the memo used 18 GHz. Applying the correction, I get a fringe rate of 6.58 Hz. The second term, , can also be quite large. Since in general can range from 1/2 step (0.625 ns) to +1/2 step (0.625 ns), for an RF frequency of 18 GHz, ranges from -4050 to 4050 degrees. It is puzzling that the total range, 8100 degrees, is not quite the same as the max degrees/step of the natural fringe term (7942.5 degrees). Ah, but the frequency 17.650 GHz does yield an exact match, which corresponds to 0 MHz in the band-34 IF, according to equation (3).















![{\displaystyle f_{LO}={\rm {FSeqList}}/2+21{\rm {[GHz]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79666c429b8194ebeca96decd8129ae720ee0e4)